© 2020 - DashTech. All Right Reserved.
Internet
Top 15 Best USE Browser Alternatives in 2024
Best and popular USE browser alternative will be discussed in this article. USE Browser is a quick web browser for...
Read moreGadgets
Entertainment
Business
Salesloft: Revolutionizing Sales Engagement Platforms
Salesloft is a groundbreaking platform that is transforming the way sales teams engage with prospects and customers. It offers a...
Best Online Fax Services For Your Business in 2024
In some cases, you need online fax services. The chances are, nevertheless, that you do not have a fax machine....
12 Best Offerup Alternatives To Use in 2024
Best Offerup Alternatives To Use will be discussed in this article. OfferUp is a free, mobile-friendly online marketplace that links...
Phones
MORE NEWS
Best Crypto Wallet For Your Digital Currency in 2024
Best crypto wallet are develop to store digital assets, take care of protection concerns like conserving secret tricks as well...
The 15 Best Manga Apps for Android Device in 2024
In this write-up, we will certainly discuss regarding best manga apps 2020, ios ideal manga app ios, manga rock application...
Top 15 Best DLNA Server Software in 2024
Best DLNA server are the sorts of house media server that we are talking about. Every web internet user wishes...
Top 19 Best Epub Reader For Windows 10 and Mac In 2024
Epub reader windows 10 data viewer software that allows you to see the digital books kept in EPUB style. Moreover,...
Best 7 Ways To Know When Print Screen Not Working
Deal With Print Screen Not Working in Windows 10?. If you want to record your desktop computer screen then what...
11 Best Online Video Chat Websites To Make Friends in 2024
In this write up, we will certainly review regarding best online video chat websites, satisfy new friends online, arbitrary video...
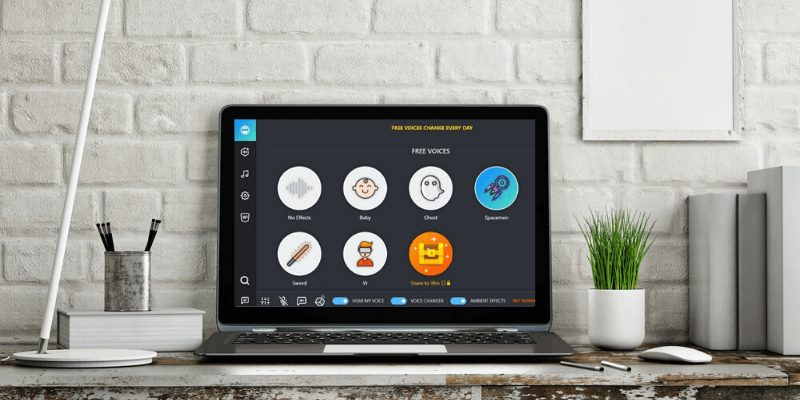
Top 15 Best Voice Changer You Should Try In 2024
A best voice changer application permits you to reproduce your voice for fun and also other thrilling functions. Perform you...