© 2020 - DashTech. All Right Reserved.
Internet
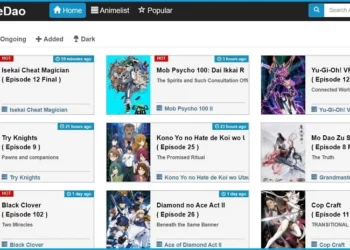
AnimeDao Alternatives 27 Sites to Watch High-Quality Anime in 2024
Are you an anime enthusiast seeking a streaming service that offers a vast collection of your favorite series and movies?...
Read moreGadgets
Entertainment
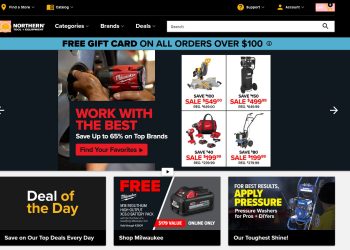
Northern Tool: Your Ultimate Destination for Tools and Equipment
Are you in need of reliable tools and equipment for your projects? Look no further than Northern Tool, the leading...
Salesloft: Revolutionizing Sales Engagement Platforms
Salesloft is a groundbreaking platform that is transforming the way sales teams engage with prospects and customers. It offers a...
Best Online Fax Services For Your Business in 2024
In some cases, you need online fax services. The chances are, nevertheless, that you do not have a fax machine....
Phones
MORE NEWS
Top 15 Best USE Browser Alternatives in 2024
Best and popular USE browser alternative will be discussed in this article. USE Browser is a quick web browser for...
12 Best Limetorrents Alternatives Working When TPB Is Down [2024]
This article contain information about limetorrent and pirate proxy 2020, limetorrent, utorrent. The preliminary gush web site on our listing...
Top 11 Best eWritingService Alternatives in 2024
Best and official eWriting service alternatives will be explained in this article. No matter what your place is, you can...
25 Best Rarbg Alternatives Working When TPB Is Down
This article contain information about Rarbg and pirate proxy 2020, qbittorrent, utorrent. The preliminary gush web site on our listing...
Top 15 Best TreeSize Alternatives in 2024
Best and most efficient Treesize alternatives will be described in this article. TreeSize is a faster disc space management platform...
Top 15 Best Freelance Skills to Master In 2024
Best and most effective freelance skills will be described in this article. To better understand how different skill sets and...
How To Sell Online In 2024
Best and effective guide how to sell online will be described in this article. Starting a Business Online There are...